At the Heart of Ring: OpenDHT — A Distributed Hash Table

This article aims to explore OpenDHT technology, briefly explain its underpinning theoretical logic, and explain why cryptography is vital to it.

The need for efficient public distributed systems is becoming increasingly important. Particularly, as the influence of the Net giants centralizing information and communications is growing exponentially, we are faced with a paradox. The Internet gives network nodes the unprecedented opportunity to exchange directly, without centralized processing point. Yet, most networks rely on centralized systems for sharing and storing data! In order to address this issue, we have developed a technology known as OpenDHT – a free and open library implementing a distributed hash table – and implemented it in our innovative decentralized communication project: Ring.

What Is A Distributed Hash Table?

DHT (distributed hash table) is a class of distributed systems that provides access to a shared dictionary of key ➛ value pairs from any node of the network where data are distributed among the participants. Currently, the most popular DHT networks such as Mainline DHT (BitTorrent) are used for peer to peer file sharing. On these networks, the key is the identifier of the torrent file – also called “Magnet links“– and the values are the IP addresses of the seeders, i.e. the clients sharing the torrent.

What Is OpenDHT?

OpenDHT is a light and robust network project DHT written in C++11 proposing a simple to use interface for application developers. Originally inspired by the DHT library developed by Juliusz Chroboczek and used, for example, by the BitTorrent client Transmission, OpenDHT includes a number of important innovations. It can store different data types; it has a listening function, and it is simple to work with.

OpenDHT provides the ability to store any type of data – not just IP addresses – with a limit value of 64 KB. It has also a listening function (listen) enabling a node to be informed of changes in key values. Since we needed these crucial features for the Ring project, we pushed to create OpenDHT with the counterparty to make its protocol incompatible with the Mainline DHT network of BitTorrent.

For the Ring project, the listen function is, for example, used to enable receiving calls or messages. This is even the case for computers behind NATs. In conjunction with the ICE technology, OpenDHT then allows the robust establishment of peer-to-peer connections.

OpenDHT is published on GitHub under the The GNU General Public License v3.0 with its earlier documentation available here. By the way, comments and patches are kindly welcomed.

OpenDHT is simple to use, thus reducing the cost and difficulty of developing applications that benefit from it. For example, starting a new node on local port 4222, and connecting to the network through a known node is as simple as these three lines written in C++:

dht::DhtRunner node; node.run(4222, dht::crypto::generateIdentity(), true);
node.bootstrap("bootstrap.ring.cx", "4222");

Then storing any value on the network is achieved with a single line of code:

node.put("my_key", std::vector(5, 10));

The key to use will then be the SHA1 condensate of the text string “my_key”. The value will be a sequence of 5 bytes worth 10.

Later retrieve this value from another node will be as simple as this:

 
node.get("ma_clé", [](const std::vector & values) { 
   for (const auto & value : values) 
      std::cout << "Valeur trouvée: " << *value << std::endl;
   return true; 
}); 

The Theory Underpinning DHTs

In the most popular type of DHT network (i.e. Kademlia) used by OpenDHT, each node (i.e. participant program) of the network has a unique identifier evenly distributed in the identifiers space – a 160-bit space in our case.

Similarly, each data stored on the network is characterized by an identifier which is its key. The keys are uniformly distributed in the same 160-bit space as the node identifiers. Multiple values can share the same key.

The binary operator XOR (⊕) is defined as the distance operator between key, or between keys and node IDs. To recap, the XOR result is true if both operands have different Boolean values. This implies that the XOR result of two 160-bit keys is the “binary distance” between these keys: A ⊕ A = 0 for every key A. For two distinct keys A and B with X = A ⊕ B, the number of zero bits at the beginning of X will be equal to the number of bits common to the beginning of A and B.

This interesting property offers the ability to partition each node’s routing table using a binary tree. In fact, each node maintains and updates a routing table including mainly the neighboring nodes (in the sense of distance of the XOR operator introduced above).

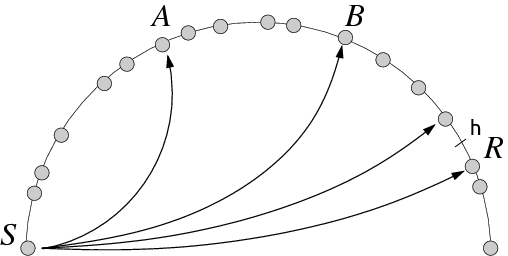
Fig. 1. To find the R node with the values for the key h (close to R), the S node contacts A which is the closest to h in its routing table. The response of A includes the IP address of B, now the closest to h in the table of S, and which is contacted, and so on.

A data element, that is to say a key-value pair (K, V), will be stored on the L nodes that are closest to key K (typically with L = 8). Any node knowing K will be able to find V by an iterative algorithm which will lead him to contact nodes whose identifiers are increasingly closer to K (Fig. 1).

Queries including the K key and the reply of each node include a list of other nodes known as closest to K. V value will be found in just O (log (N)) iterations — N representing the number of nodes on the network.

Cryptography: A Critical Step in Network Security

Just like the Internet, public DHT are inherently unreliable networks. They involve trusting many other programs randomly on the network to store data.

Instead of trying to make the protocol resistant and withstanding any type of malicious node, which would be illusive, the OpenDHT approach is to consider the network itself as untrustworthy and build over an optional cryptographic layer public key, using the Public Key Cryptography Standards (PKCS) infrastructure, and to verify the author and message integrity (signature) and encrypt the latter with public certificates published on the DHT network.

Knowing the identifier of the contact_id public key of a contact, storing an encrypted data for this contact on the DHT network is as simple as:
Ring

node.putEncrypted("my_key", contact_id, value);

The cryptography layer (or identity layer) then will transparently retrieve the certificate of the contact, use the public key to encrypt the data, and then store it on the network.

This layer will also transparently check the signature of signed data received. If the check fails, the data is not presented to the application. Similarly, only encrypted data that can be decrypted are passed to the application.

Ring implements these cryptographic operations to securely exchange invitations, initiation of calls and private messages. The network can therefore be realistically used as a public meeting place – making Ring a truly distributed universal communication platform.

For further information: