Au cœur de Ring : OpenDHT, une table de hachage distribuée de nouvelle génération

Cet article a pour but d’explorer la technologie OpenDHT, d’aborder brièvement sa logique théorique sous-jacente et d’expliquer en quoi la cryptographie est un élément qui lui est vital.

Le besoin de systèmes distribués publics efficaces se fait de plus en plus pressant. Alors que grandit chaque jour l’influence des géants du Net qui centralisent plus que jamais l’information et les communications, nous sommes face à un paradoxe. En effet, Internet offre aux nœuds du réseau la possibilité inédite de se contacter directement, sans point de traitement centralisé. Pourtant, la majorité des réseaux repose sur des systèmes centralisés pour le stockage et le partage de données ! Pour répondre à cette problématique, nous avons développé la technologie OpenDHT – une bibliothèque logicielle sous licence libre implémentant une table de hachage distribuée – que nous avons par la suite intégré au cœur de notre système de communication décentralisé : Ring.

Qu’est-ce qu’une table de hachage distribuée ?

Le DHT (table de hachage distribuée) est une classe de systèmes distribués permettant d’accéder, depuis tout nœud du réseau, à un dictionnaire partagé de paires clé➛valeur dont les données sont réparties entre les participants. Actuellement, les réseaux DHT les plus populaires comme Mainline DHT (BitTorrent), sont utilisés pour le partage de fichiers de pair à pair. Sur ces réseaux, la clé est l’identifiant du fichier torrent, aussi appelé « lien Magnet », et les valeurs sont les adresses IP des seeders, c’est à dire les clients partageant le torrent.

Qu’est-ce que OpenDHT ?

OpenDHT est un projet de réseau DHT léger et robuste en C++11 proposant une interface simple à utiliser pour les développeurs d’applications. Inspiré à l’origine de la bibliothèque DHT développée par Juliusz Chroboczek et utilisée, par exemple, par le client BitTorrent Transmission, OpenDHT inclus un certain nombre d’innovations importantes.

OpenDHT offre la possibilité de stocker tout type de données — pas seulement des adresses IP — avec une limite par valeur de 64 Ko. Il offre également une fonction d’écoute (listen), permettant à un nœud d’être informé des changements de valeurs concernant une clé. Le besoin de ces fonctionnalités cruciales pour le projet Ring nous ont poussé à créer OpenDHT, avec la contrepartie de rendre son protocole incompatible avec le réseau DHT Mainline de BitTorrent.

Concernant le projet Ring, la fonction listen est par exemple utilisée pour permettre de recevoir des appels ou des messages, même pour des ordinateurs situés derrière des NATs. En conjonction avec la technologie ICE, OpenDHT permet alors l’établissement de connections pair à pair de manière robuste.

OpenDHT est publié sur GitHub sous licence GPL version 3 avec un début de documentation disponible ici. Commentaires et correctifs sont les bienvenus.

OpenDHT se veut simple à utiliser, réduisant ainsi le coût et la difficulté du développement des applications qui en tirent parti. Par exemple, lancer un nouveau nœud sur le port local 4222, puis se connecter au réseau à travers un nœud connu est aussi simple que ces trois lignes écrites en C++ :

dht::DhtRunner node; node.run(4222, dht::crypto::generateIdentity(), true);
node.bootstrap("bootstrap.ring.cx", "4222");

Stocker une valeur quelconque sur le réseau est alors possible en une unique ligne de code :

node.put("ma_clé", std::vector(5, 10));

La clé utilisée sera alors le condensat SHA1 du texte ma_clé. La valeur sera une suite de 5 octets valant 10.

Récupérer par la suite cette valeur depuis un autre nœud sera alors aussi simple que :

node.get("ma_clé", [](const std::vector & values) {
  for (const auto &; value : values)
    std::cout << "Valeur trouvée: " << *value << std::endl;
  return true;
});

La théorie sous-jacente aux DHTs

Dans le type de réseau DHT le plus populaire (Kademlia), utilisé par OpenDHT, chaque nœud (programme participant) du réseau possède un identifiant unique uniformément distribué dans l’espace des identifiants — un espace de 160 bits, dans notre cas.

De même, chaque donnée stockée sur le réseau est caractérisée par un identifiant : sa clé. Les clés sont uniformément distribuées dans le même espace de 160 bits que les identifiants de nœud. Plusieurs valeurs peuvent partager une même clé.

L’opérateur binaire XOR (⊕) est défini comme l’opérateur de distance entre clés, ou entre clés et identifiants de nœud. Pour rappel, le résultat de XOR est vrai si les deux opérandes ont des valeurs booléennes distinctes. Ceci implique que le résultat du XOR de deux clés de 160 bits représente la « distance binaire » entre ces clés : A ⊕ A = 0 pour toute clé A. Pour deux clés distinctes A et B avec X = A ⊕ B, le nombre de bits à zéro au début de X sera égal au nombre de bits communs au début de A et B.

Cette propriété intéressante offre la possibilité de partitionner la table de routage de chaque nœud en utilisant un arbre binaire. Chaque nœud maintient à jour, en effet, une table de routage incluant principalement les nœuds voisins (au sens de l’opérateur de distance XOR introduit ci-dessus).

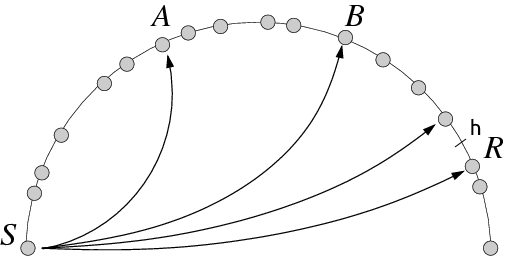
Fig. 1. Pour trouver le nœud R possédant les valeurs pour la clé h, le nœud S contacte A, le nœud plus proche de h dans sa table de routage. La réponse de A inclut l’adresse IP de B, maintenant le plus proche de h dans la table de S et qui est donc contacté, et ainsi de suite.

Une donnée, c’est-à-dire une paire clé-valeur (K, V), sera alors stockée sur les L nœuds les plus proches de la clé K (avec typiquement L = 8). Tout nœud connaissant K pourra alors retrouver V par un algorithme itératif qui l’amènera à contacter des nœuds dont l’identifiant est de plus en plus proche de K (fig. 1).

Les requêtes incluent la clé K et la réponse de chaque nœud comprend une liste des autres nœuds connus les plus proches de K. La valeur V sera alors retrouvée en seulement O(log(N)) itérations, N représentant le nombre de nœuds sur le réseau.

Cryptographie : Une étape critique dans la sécurité des réseaux

Tout comme Internet, les DHT publiques sont par nature des réseaux non-fiables. Ils impliquent de faire confiance à un grand nombre d’autres programmes au hasard sur le réseau pour stocker des données.

Plutôt que de tenter de rendre le protocole robuste à tout type de nœud malveillant, ce qui serait illusoire, l’approche d’OpenDHT est de considérer le réseau lui-même comme non digne de confiance et de construire par dessus une couche optionnelle de cryptographie à clé publique, utilisant l’infrastructure standard PKCS (Public-Key Cryptography Standards), ou standards de cryptographie à clé publique, et permettant de vérifier l’auteur et l’intégrité du message (signature) et de le chiffrer grâce aux certificats publiques publiés sur le réseau DHT.

Connaissant l’identifiant de la clef publique contact_id d’un contact, stocker sur le réseau DHT une donnée chiffrée pour ce contact est aussi simple que :

node.putEncrypted("ma_clé", contact_id, value);

La couche de cryptographie, ou couche d’identité, va alors récupérer, de manière transparente, le certificat du contact, utiliser la clef publique pour chiffrer la donnée, puis la stocker sur le réseau.

Cette couche va, également de manière transparente, vérifier la signature des données signées reçues. Si la vérification échoue, la donnée n’est pas présentée à l’application. De même, seules les données chiffrées qu’il est possible de déchiffrer sont remontées à l’application.

Ring utilise ces opérations de cryptographie pour échanger de manière sécurisée les invitations, les initiations d’appels et messages privés. Le réseau est alors utilisé comme un point de rencontre public, faisant ainsi de Ring une  plateforme de communication universelle distribuée.